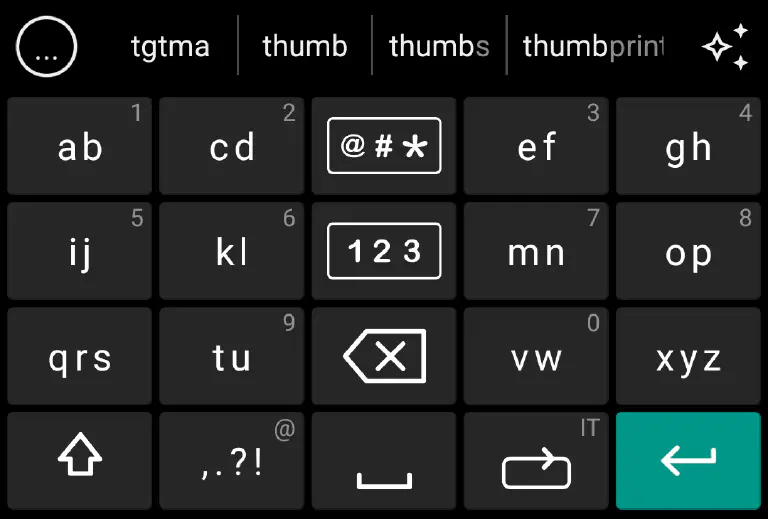
Have you ever seen this kind of keyboard before? This is a keyboard that is widely used across Byteland, where most of the people use Bytephones, so most of the people call it “Bytephone Keyboard”. It is a great intellectual invention which made typing Bytish much easier.
There are $K$ different characters in Bytish, numbered from $1$ to $K$. Bytish words are composed of exactly three letters, for a word $W$, the three letters are $W_1$, $W_2$ and $W_3$ accordingly. There are $M$ words in the Bytish dictionary, of which the $i^{th}$ one is $S_i$. It is not guaranteed that all the $M$ words are distinct.
The keyboard contains $N$ keys, numbered from $1$ to $N$, where the $i^{th}$ key is a combination of a continuous range of characters from $L_i$ to $R_i$. Typically, $L_1 = 1$ and $R_N = K$, $R_i + 1 = L_{i+1}$ for every $1 \le i \lt N$, which means that every character is covered by exactly one key, and the keys are arranged in ascending order of characters.
After pressing three keys, the Bytephone shows you all of the matching words of the 3-key combination from the dictionary. Formally, let the 3-key combination be key number $A$, $B$ and $C$, for a word $W$ to be a matching word of this 3-key combination, it must satisfy $L_A \le W_1 \le R_A$ and $L_B \le W_2 \le R_B$ and $L_C \le W_3 \le R_C$. For example, words 1 5 4 and 2,6,3 are matching words of the 3-key combination $([1,2],[5,6],[3,4])$, but words 1 3 4 or 3 4 2 are not.
You have to answer $Q$ queries through reverse engineering with this keyboard: given that the word $T$ is one of the matching word of an unknown 3-key combination ($T$ may not be in the dictionary), find out the number of matching words from the dictionary that is a matching word of the unkown 3-key combination.
Input Specification
The first line contains two integers $N$ and $K$.
The next line contains $N$ integers, where the $i^{th}$ one is $L_i$.
The next line contains $N$ integers, where the $i^{th}$ one is $R_i$.
The next line contains an integer $M$.
The next $M$ lines contains the word $S_i$, which is three positive integers $S_{i,1}$, $S_{i,2}$ and $S_{i,3}$ in order.
The next line contains an integer $Q$.
The next $Q$ lines contains the word $T$ for the $i^{th}$ query on the $i^{th}$ line, which are three positive integers $T_1$,$T_2$ and $T_3$.
Output Specification
Output $Q$ lines, where the answer of the $i^{th}$ query is on the $i^{th}$ line.
Subtasks
For all cases,
$1 \le N,M,Q \le 2 \times 10^5$
$1 \le N \le K \le 10^9$
$1 \le L_i \le R_i \le K$ for every $1 \le i \le N$
$L_1 = 1$ and $R_N = K$, $R_i + 1 = L_{i+1}$ for every $1 \le i \lt N$
$1 \le S_{i,1}, S_{i,2}, S_{i,3} \le K$ for all $1 \le i \le M$
$1 \le T_1, T_2, T_3 \le K$
Subtask 1: $L_i = R_i$ for every $1 \le i \le N$ (30 pts)
Subtask 2: $1 \le N,M,Q \le 1000$ (30 pts)
Subtask 3: $1 \le N \le 100$ (30 pts)
Subtask 4: No additional constraints (10 pts)
Sample Test Cases
| Input | Output | |
|---|---|---|
| 3 9 1 4 7 3 6 9 3 2 6 8 1 5 7 3 7 9 1 2 5 9 |
2 | |
The 3 keys corresponds to charaters of ranges $[1,3]$, $[4,6]$, $[7,9]$.
Through reverse engineering, the unknown 3-key combination is to the only query |
||
| 3 9 1 4 7 3 6 9 8 2 6 8 1 5 7 4 9 1 6 4 5 4 6 8 5 4 9 4 6 6 3 4 9 5 2 5 8 6 8 3 5 4 7 5 5 5 2 6 8 |
3 1 2 2 3 |
|
Scoring: Per Subtask
Authored by wy24215
Appeared in 2026 Mini Comp 1 [WY Interschool Pre-CCC]